Řešení křížovek:
ŠIKMO DOLŮ ZLEVA DOPRAVA: 1. Né. - 2. Tín; gebis. - 3. Jihoafrický; ot; Donnie. - 4. Prodělat; Eames; kája; S; Poti; Raud. - 5. IVV; sitcomy; letos; ete. – 6. D; biotika; pelagra; NAIA; Éset. - 7. Rytmika; GeO; ki; Kovic; C klíč. - 8. Napellin; Al; mat; Doorn; gir. - 9. Piastrino; Áli; i; Rak; statistky; kylit; loje. - 10. KUBALKO; okna; potravy; opavy; nonetit; anomer. - 11. Strokač; vařiti s invalidem; odvary z makovic; rod much; lm. - 12. Opidum; lachtan; kočkodani; usmátý. - 13. Krahulí; cesta do práce. – 14. Skoro; kainisti; bradykardie; otepina. - 15. East; Linnean; Trivikrama. - 16. Kručov; neslosovati; epizoa; rarara (tarara). - 17. Skár; Sárinka; dosti častý; inam; bitovati; raný. - 18. Skotom + Skotovo rodisko; tmavší; inion; bi; podena; Važice. - 19. Proud; Benguelský; dorsit; suna; líce. - 20. Ka; enucleatio; udokanit; stlum; kan. - 21. Tobros; viset na nitce; stoper. - 22. Vale; kalodendron (ledodendron); Kiton; vtem. – 23. Roka; vodní savec. - 24. Stouliti se. - 25. Kapsa; sterkus; cirkus. – 26. Obrokový (rébusově); Mba; cija. – 27. Naokolo (rébusově); Luba; TNK. – 28. Napredak. – 29. Procna.
Tajenky: 1. Lachtan jihoafrický. – 2. Vodní savec. – 3. Studený Benguelský proud. – 4. Dva kilogramy potravy. – 5. Bradykardie. – 6. Imunologické studie.
Řešení hádanek:
1. Ilustrace Smetany – starý tulení samec. - 2. Množiny, bylo (byla) zima, lokty – mroži ryby loví málokdy. - 3. Potlach, nechvála, áčko u skal – po lachtanech vlasáč koukal. - 4. Otarie, tuleni (písmena před a po písmenech s háčkem). - 5. Cep, čolci, Hanák řve, věty – čepcol číhá na krevety. - 6. Chalan za natíráním, Dorka – na lachtana zírá nimrodka.- 7. „Rypouše našinec vyplaší,“ tuší neť. - 8. Vor, suma, kupcové čelo – v soumraku čepcolové. - 9. Plachta, hnízdo, hlava jízdy (jízd), září, slepota, spění – lachtani zdolávají zdařile potápění. - 10. Fistule, minima, látka – tulení matka.
Řešení logických úloh:
1. Skrývačka
Čtyřka.
Obrázky lachtana jsou totožné vždy až na jednu čárku. Ta se skrývá za sedmero čarami za uchem lachtana. Superpozicí (složením tří vyobrazených lachtanů na sebe) se nad ploutví objeví čtyřka. Nutno podotknout, že řešitelé odhalili vícero dalších logicky zdůvodněných čísel a všechny jsem uznával (300 jako CCC římskými číslicemi, 8 jako německy acht ve slově lachtani atd.).
2. Lachtaní šou
Čtyři různá řešení:
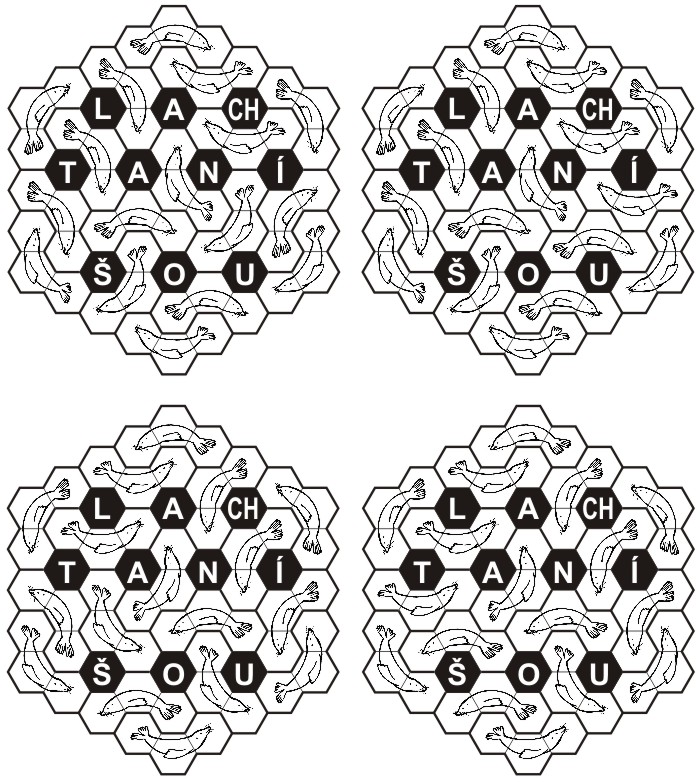
3. Řada čísel
Geometrickým tělesem je anuloid (torus, kruhový prstenec). Řada čísel je 2, 6, 13, 24, 40 atd. Pomocí vzorce (1n³ + 3n² + 8n)/6 se pro n rovinných řezů anuloidu dá zjistit největší možný počet dílů anuloidu dosažitelný těmito řezy. Což o to, u jednoho řezu je to jasné. I u dvou šikmých řezů proti sobě si umíme představit čtyři kousky „dortu“ a dva velké oblouky. Tři řezy musejí být vedeny šikovně ve správných úhlech a jdou ještě solidně zobrazit graficky. Řešitelé došli logickým postupem k řadě čísel i k podobě vzorce. Troufám si tvrdit, že zpaměti nikdo z nich neznal, co je to za vzorec. Ale ruku na srdce, znáte zpaměti třeba vzorec pro objem pravidelného osmistěnu či kulové úseče? Samozřejmě si řešitelé pomohli hledáním na internetu. U korespondenčních soutěží je to přece také o hledání a nalézání. I při hledání je třeba zapojit logické myšlení. Když zadáte na google v rozšířeném vyhledávání do kolonky Najít výsledky s přesnou frází naši řadu čísel 2, 6, 13, 24, 40 a do kolonky Najít výsledky s alespoň jedním ze slov cutting (anglicky řezání), pak všechny tři nalezené odkazy vedou k anuloidu. Pokud místo cutting zadáte parts (anglicky části) nebo geometric (anglicky geometrické), opět dojdete k cíli. A také napomohl připojený obrázek delfína proskakujícího kruhovým prstencem (anuloidem, torem). Při zadání naší řady a slova torus jste byli ve vyhledávačích u cíle ihned.
4. Rypouš
Nejkratší cesta vede přes 68 polí, existují dvě různá řešení (viz obrázky).
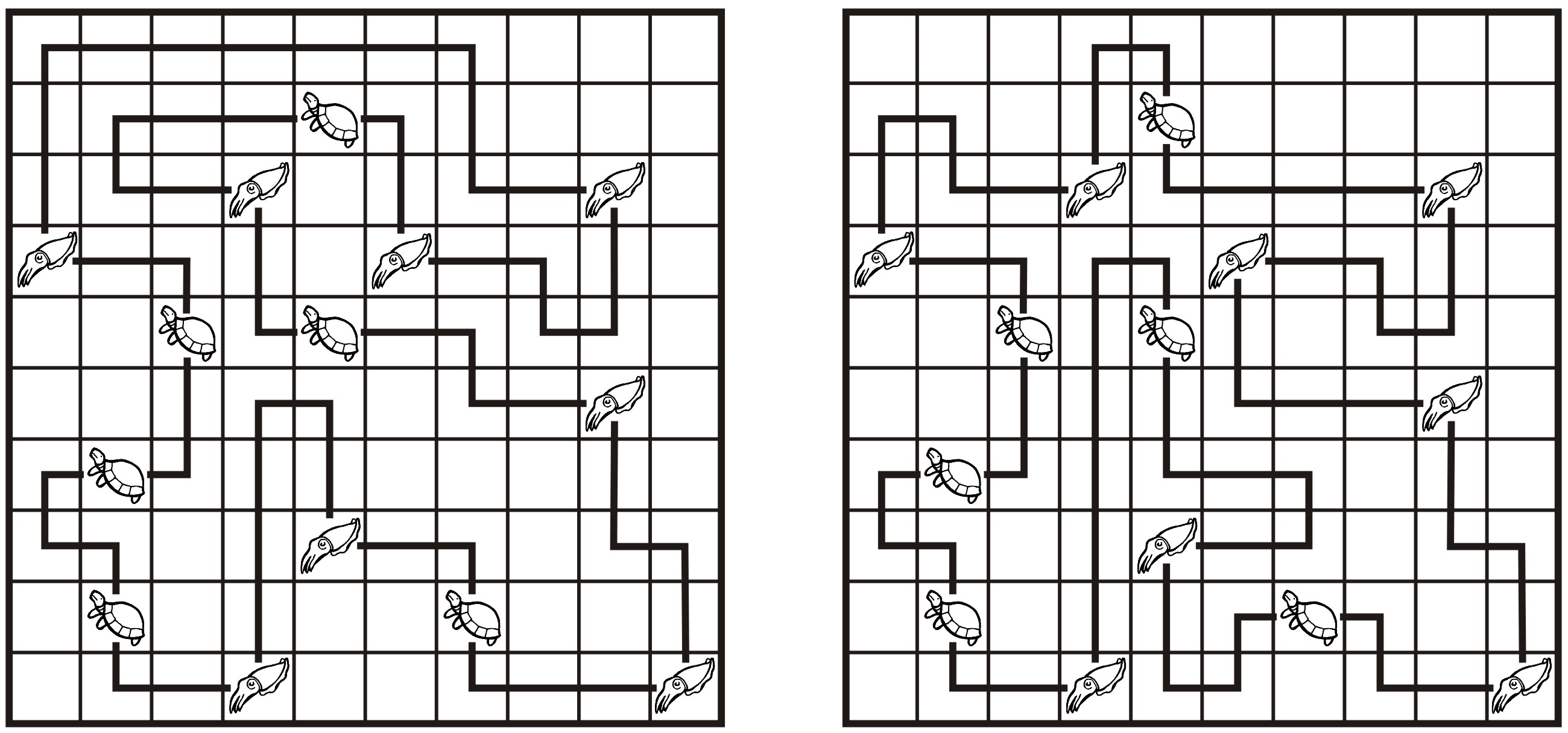
5. Kry
Při nepřevracení ker vejde do rastru 11 lachtanů, při převracení ker dokonce 12. Že nejde přímo o lachtany, na to většina řešitelů přišla, protože ty lze umístit na kry, každého na svou nebo jakkoli jinak, i pod kry. Šlo o to umístit do rastru co nejvíce ker (viz obrázky).
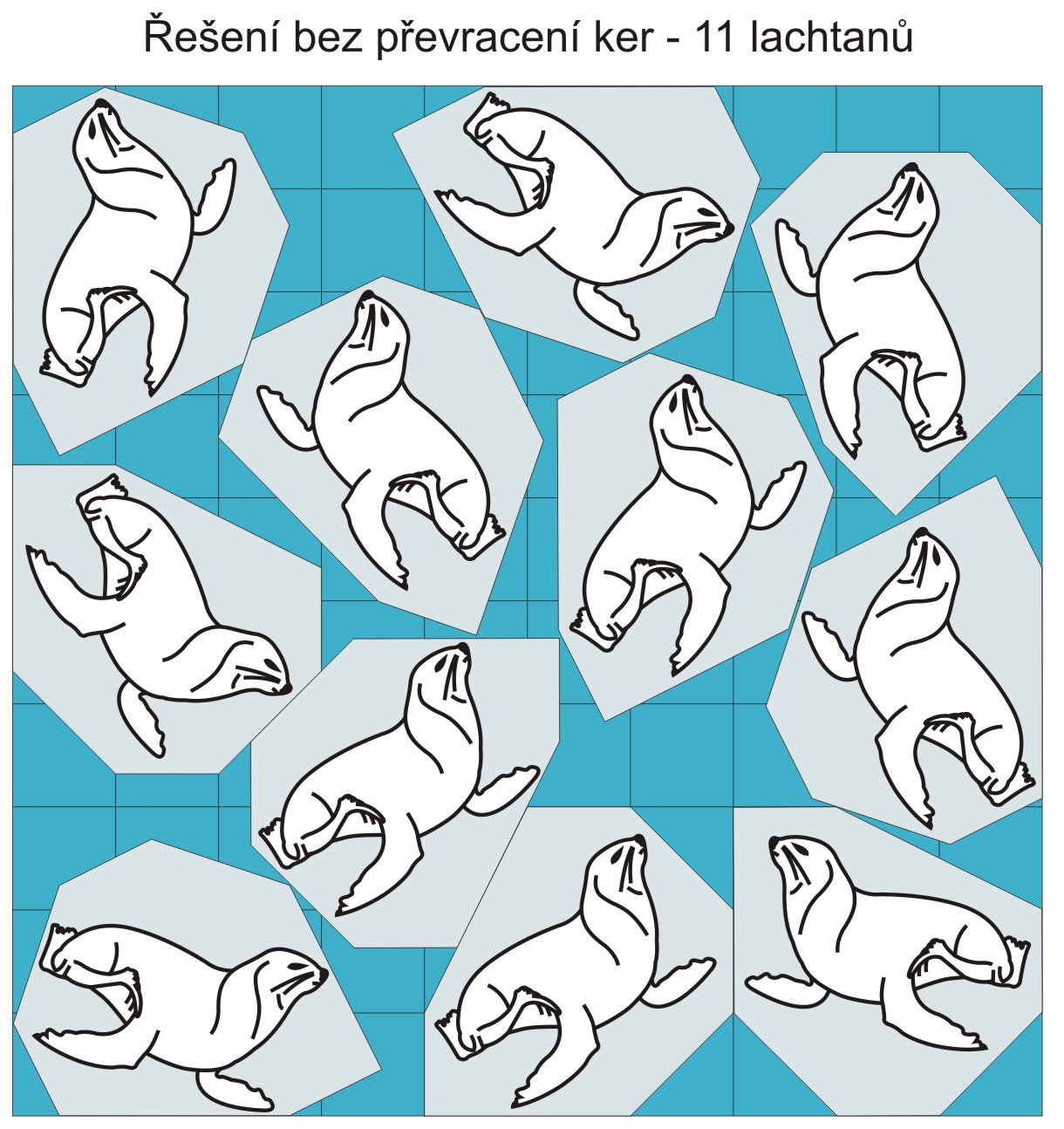
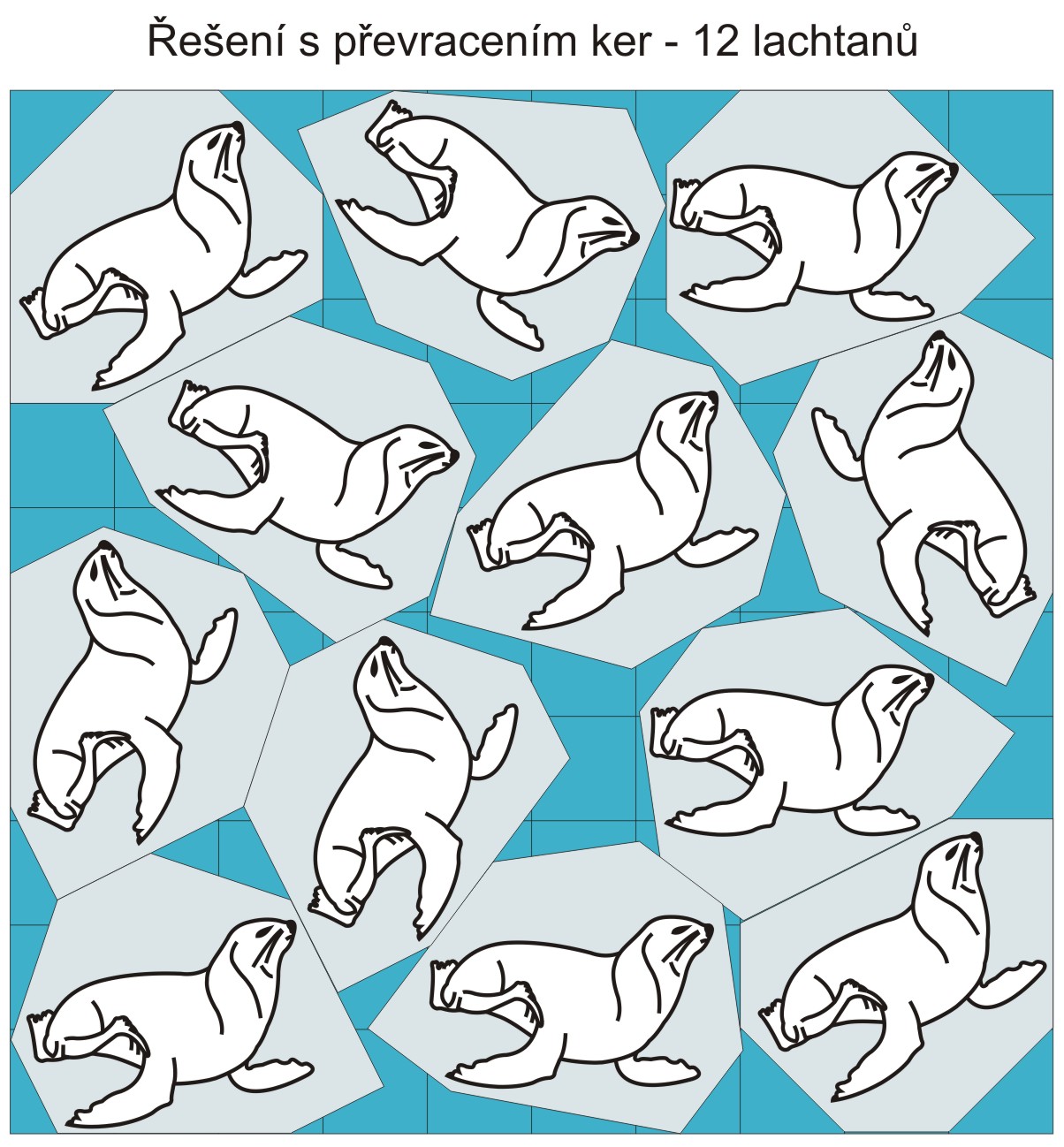
6. Plavidla na moři
Řešení viz obrázek.

7. Ploutvonožci
Údaje o hmotnostech jsou uvedeny v šestkové číselné soustavě a mladší mládě váží 144 kg. Rozhodující pro správné řešení byla hmotnost dospělé samice, která v přírodě dosahuje hmotnosti od 250 kg do jedné tuny. Pokud by údaje o hmotnostech byly uvedeny v devítkové soustavě, pak by hmotnost mladšího mláděte vycházela 486 kg, což u mláděte samce by bylo stále reálné, ovšem hmotnost dospělé samice 1 944 kg je zcela mimo realitu!
Řešení:
Mladší mládě váží 10x jednotek, starší 20x, samice 40x a samec 105 x – desítky jsou tam kvůli tomu, abychom nepočítali s desetinnými čísly, když je budeme převádět do různých číselných soustav. Dostáváme rovnici v desítkové číselné soustavě
120x – 1000 = 105x
15x = 1000 |.7
105x = 7000 |hmotnost samce
Počítat můžeme začít až od čtverkové číselné soustavy nahoru, protože trojnásobek hmotnosti v nižších soustavách neexistuje. Ve čtverkové je rovnice takováto
1221x = 13000 |hmotnost samce,
převedeno do desítkové soustavy znamená u samce hmotnost 448 kg, u samice a mláďat vyjde hmotnost v necelých číslech. Podobně v pětkové číselné soustavě. V šestkové takto
253x = 11000 |hmotnost samce,
převedeno do desítkové soustavy znamená u dorůstajícího samce hmotnost 1512 kg, u samice 576 kg, u staršího mláděte 288 kg a u mladšího mláděte 144 kg, což odpovídá i realitě v přírodě (dospělí samci dosahují hmotnosti dvou až pěti tun, samice hmotnosti 250 kg až tuny). V sedmičkové a osmičkové číselné soustavě u samice a mláďat nevyjdou celá čísla hmotností, v devítkové číselné soustavě je rovnice takováto
126x = 7000 |hmotnost samce,
což převedeno do desítkové soustavy znamená u samce hmotnost 5103 kg, což by ještě u samce šlo s přimhouřením oka tolerovat, neboť v přírodě dosahují samci rypouše sloního hmotnosti až pěti tun. Ovšem zcela nereálná hmotnost 1944 kg by vycházela u samice, ty v přírodě u rypouše sloního dosahují hmotnosti maximálně kolem tuny. V každé další vyšší číselné soustavě by hmotnosti vycházely ještě vyšší a tudíž ještě více nereálné.
8. Tuleni
Jedno z možných řešení viz obrázek.
.jpg)
Novinky
JEMELÍKOVA LUŠTITELSKÁ AKADEMIE - JLA 2024
JLA je dlouhodobá kombinovaná soutěž v řešení křížovek, háda- nek a logických úloh o ceny v eu- rech, kvalifikační body a v rámci recesistické části též o akade- mické tituly JLA. Na stránce JLA 2024 naleznete soutěžní podmínky, na stránce pomůcky k JLA naleznete mj. prameny použité v tom kterém kole JLA, nechybí ani recesistická část JLA a promoce JLA. 72. kolo JLA probíhá od 25. dubna do 23. května 2024, můžete si otevřít kompletní zadání 72. kola JLA, nebo jen zadání křížovky 72. kola JLA, zadání hádanek 72. kola JLA či zadání logických úloh 72. kola JLA. Hodně zdaru a zábavy při řešení, Vladimír
JLA 2022
Vše o 66. až 70. kole JLA zjistíte na JLA 2022, kola byla věnována valašským výrobkům hotoveným z proutí. Křížovkáři řešili postupně koš, opálku, kukaň, stoličku a kufr, hádankáři a logici taje a úlohy s nimi spojené.
JLA 2021
Vše o 61. až 65. kole JLA zjistíte na JLA 2021, kola byla věnována valašským doma vyráběným dřevěným výrobkům. Křížovkáři řešili postupně metlu, hrábě, vidle, motyku a lopatu, hádankáři a logici taje a úlohy s nimi spojené.
JLA 2020
Vše o 56. až 60. kole JLA zjistíte kliknutím na JLA 2020, křížovkáři řešili dřevěný hák užívaný k orání, pěší saně pro svoz dřeva, sečkovici, geletu na dojení ovcí a lis na tvaroh, hádankáři a logici taje a úlohy spojené s oráním, sáňkováním, výrobou sečky, dojením a lisováním tvarohu.
JLA 2019
Vše o 51. až 55. kole JLA zjistíte kliknutím na JLA 2019, křížovkáři řešili papuče, plť, kvíčalu, tkalcovskou destičku ke snovadlům a část valchovacího zařízení, hádankáři a logici taje a úlohy spojené s papučáři, plťaři, ptáčníky, tkalci a valcháři.
JLA 2018
Vše o 46. až 50. kole JLA zjistíte kliknutím na JLA 2018, křížovkáři řešili barvířskou nádobu, brousek, fajfku, formanskou truhlici a křivák, hádankáři a logici taje a úlohy spojené s barvíři, brouskaři, fajfkaři, formany a křiváčkáři.
JLA 2017
Vše o 41. až 45. kole JLA zjistíte kliknutím na JLA 2017, křížovkáři řešili struhadlo na zelí, palici na tlučení brambor, sekáček na maso, oválnou desku na maso a dřevěné tvořítko na cukroví, hádankáři a logici taje a úlohy spojené se zelím, bramborami, masem, zabijačkou a Vánocemi.
JLA 2016
Vše o 36. až 40. kole JLA zjistíte kliknutím na JLA 2016, křížovkáři řešili ošatku na chleba, lopatku na koláče, cedník na nudle, lžičku na kaši a talíř na polévku, hádankáři a logici taje a úlohy s nimi spojené.

JLA 2015
Vše o 31. až 35. kole JLA zjistíte kliknutím na JLA 2015, křížovkáři řešili lyžičník, hmoždíř, máselni- ci, solničku a čerpák, hádankáři a logici taje a úlohy s nimi spojené.

JLA 2014
Vše o 26. až 30. kole JLA zjistíte kliknutím na JLA 2014, křížovkáři řešili dětskou káču, klepač, kolečko, pastýře s ovečkou a sáňky, hádankáři a logici taje a úlohy spojené s těmito dětskými hračkami.

JLA 2013
Vše o 21. až 25. kole JLA zjistíte kliknutím na JLA 2013, křížovkáři řešili bodloka, želvu, žaka, kapy- baru a surikatu, hádankáři a logi- ci taje a úlohy spojené s ostno- ploutvými rybami, želvami, pa- poušky, kapybarami a promyko- vitými.
.jpg)
JLA 2012
Vše o 16. až 20. kole JLA zjistíte kliknutím na JLA 2012, křížovkáři řešili vlka, pekariho, kozorožce, losici a morče, hádankáři a logici hádanky a úlohy spojené s psovitými šelmami, nepřežvýka- vými, turovitými, jelenci a diko- brazočelistními.
JLA 2011
Vše o 11. až 15. kole JLA zjistíte kliknutím na JLA 2011, křížovkáři řešili lachtana, bobra, sovici, medvědici a dželadu, hádankáři a logici hádanky a úlohy spojené s ploutvonohými, bobry, sovami, medvědy a úzkonosými opicemi.
JLA 2010
Vše o 6. až 10. kole JLA zjistíte kliknutím na JLA 2010, křížovkáři řešili pět valašských kapliček, hádankáři a logici hádanky a úlohy spojené s jejich patrony.
JLA 2009
Vše o prvých pěti kolech JLA zjistíte kliknutím na JLA 2009, křížovkáři řešili pět maskotů LOH 2008, hádankáři taje z oblasti sportů a logici úlohy s tématikou vody, lesu, ohně, země a oblohy.
MLSK 2008 A JLA 2010 - Z KOSTELA A KAPLÍ VZNIKLY TAKÉ OBRAZY

Křížovkářské zpracování Kostela Panny Marie Sněžné ve Velkých Karlovicích bylo umístěno nad nástěnkou nalevo od kříže v zádveří kostela, napravo od něj byla křížovkářská zpracování Kaple sv. Floriána ve Velkých Karlovicích - Léskovém a Kaple Panny Marie Růžencové ve Velkých Karlovicích - Podťatém. Obrazy jsou umístěné v sídle ČSHAK.
MLSK 2007 - DŘEVORUBEC SE STAL SLAVNÝM

Křížovkářské zpracování obrazu Dřevorubec bylo zařazeno agenturou Dobrý den do Muzea rekordů a kuriozit v Pelhřimově.
.jpg)








.jpg)

